
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
✿♥‿♥✿ Видеоматериалы по темам Вероятности и статистики ✿♥‿♥✿
ˏˋ°•*⁀➷ Тема 1: Элементы комбинаторики
Перестановки без повторений:
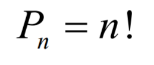
Сочетания без повторений:
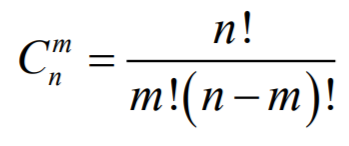
Размещения без повторений:
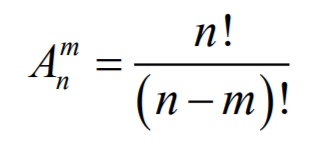
Перестановки с повторениями:
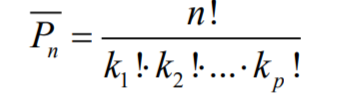
Сочетания с повторениями:
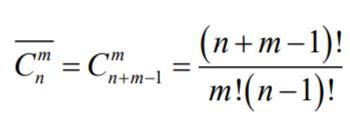
Размещения с повторениями:
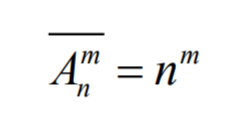
Перестановки без повторений:
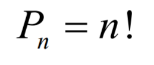
Перестановки с повторениями:
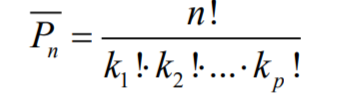
Сочетания без повторений:
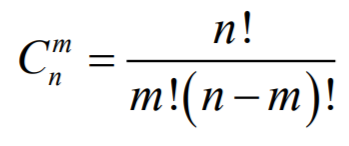
Сочетания с повторениями:
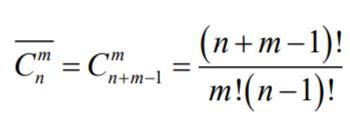
Размещения без повторений:
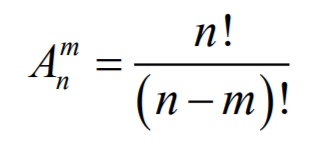
Размещения с повторениями:
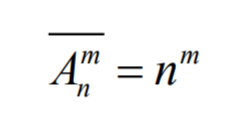
ˏˋ°•*⁀➷ Тема 2: Классическое определение вероятности
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события А обозначают через Р(А) (здесь Р - первая буква французского слова probabilite - вероятность). В соответствии с определением
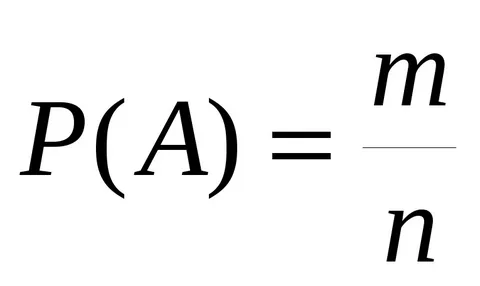
m - число элементарных исходов, благоприятствующих событию А
n - число всех равновозможных элементарных исходов опыта, образующих полную группу событий
ˏˋ°•*⁀➷ Тема 3: Теорема сложения вероятностей
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
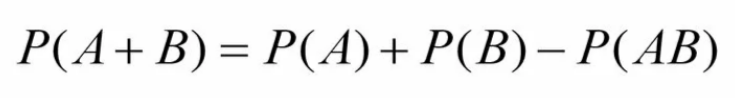
Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий:
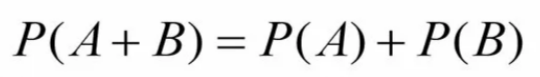
ˏˋ°•*⁀➷ Тема 4: Теорема умножения вероятностей
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого:
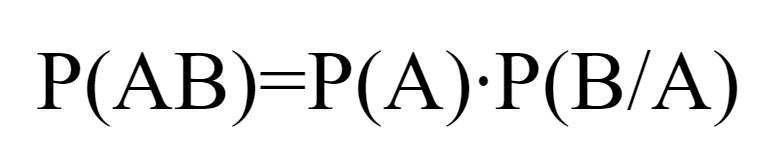
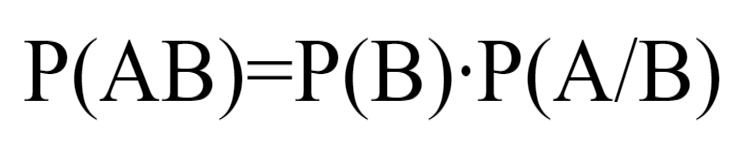
Если A и B независимые события, то:
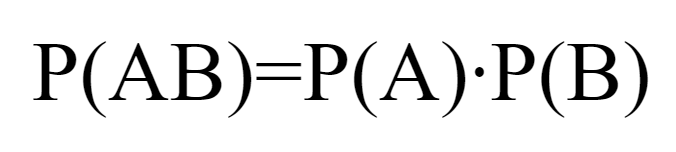
ˏˋ°•*⁀➷ Тема 5: Формула полной вероятности и формула Байеса
Пусть H1, Н2, …, Hn попарно несовместные события, образующие полную группу (т.е. сумма вероятностей этих событий =1). Будем называть их гипотезами.
Событие А – событие, которое может наступить при условии, что наступило одно из событий-гипотез (A/Hi).
Формула полной вероятности:
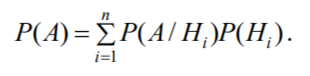
Формула Байеса:
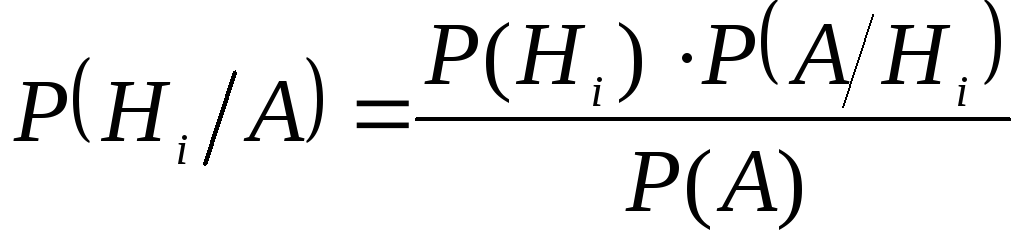
где P(A) – полная вероятность
P(Hi/A) - вероятность гипотезы, при условии, что событие А произошло.
ˏˋ°•*⁀➷ Тема 6: Формула Бернулли
Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события определённое количество раз при любом числе независимых испытаний. То есть, это вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления равна P, событие наступит ровно К раз.
Формула справедлива только для тех независимых испытаний, в которых вероятность события сохраняется постоянной!
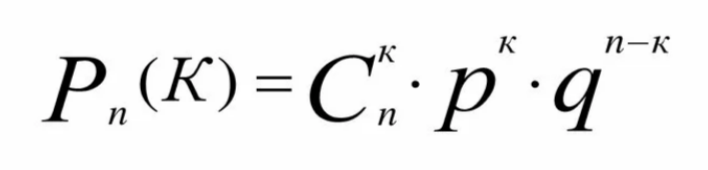
где q - вероятность противоположного события: q=1-p
ˏˋ°•*⁀➷ Тема 7: Локальная теорема Лапласа
Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Рₙ(m) того, что событие А появится в п испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n)
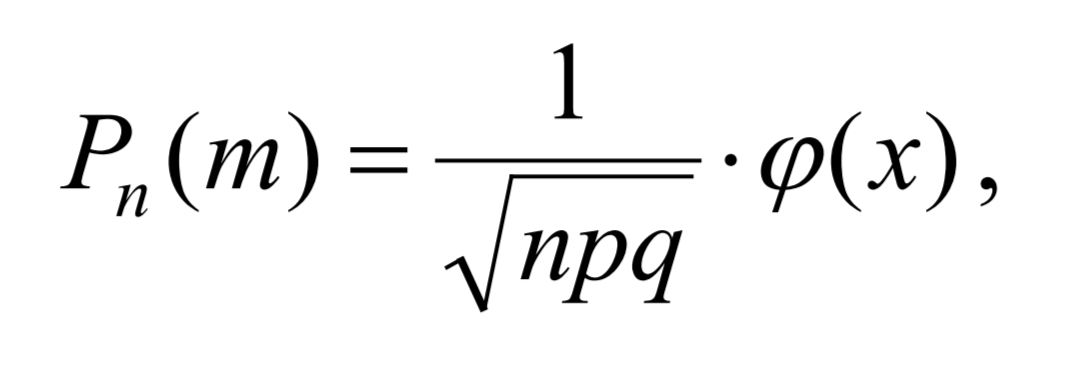
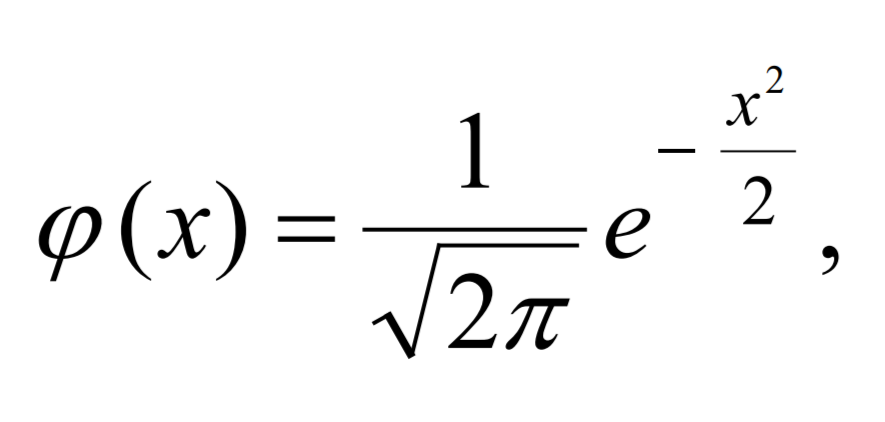
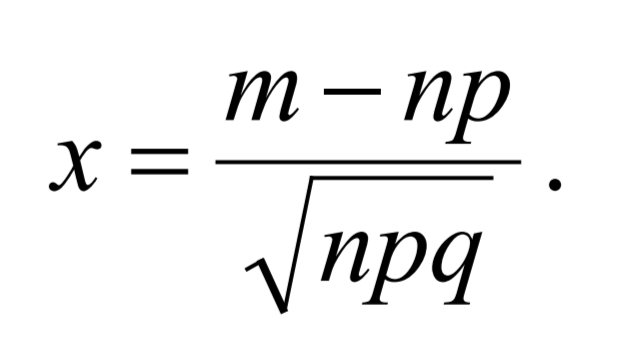
ˏˋ°•*⁀➷ Тема 8: Интегральная теорема Лапласа
Если вероятность р наступления события А в каждом испытании постоянна (0<<1), то вероятность того, что число к наступлений события А в n независимых испытаниях заключено в пределах от K1, до К2 при достаточно большом числе и приближенно равно:
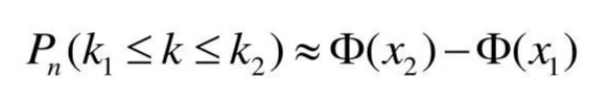
В этой формуле:
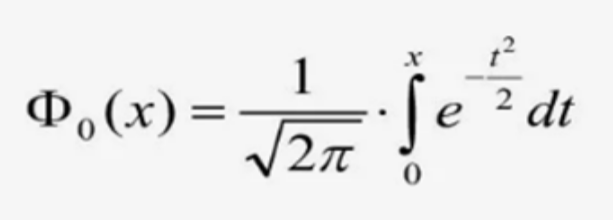
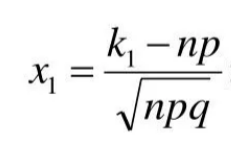
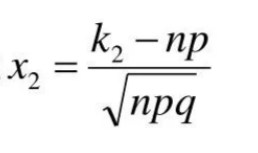
ˏˋ°•*⁀➷ Тема 9: Формула Пуассона
Теорема. Если вероятность р наступления события А в каждом испытании постоянна и мала, а число независимых испытаний п достаточно велико, то вероятность того, что событие А наступит m раз приближенно равна:
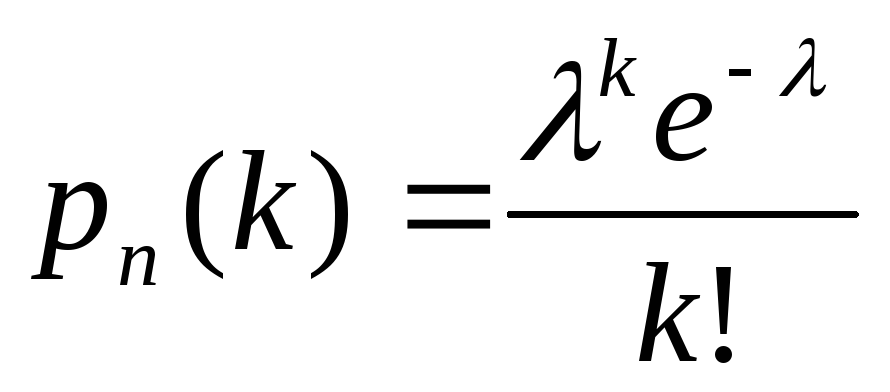
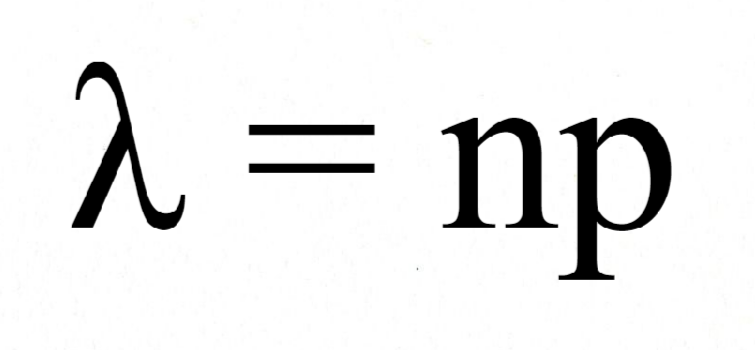
ˏˋ°•*⁀➷ Тема 10: Дискретные случайные величин
Случайной величиной называется величина, которая в результате опыта принимает то или иное числовое значение, причем заранее, до опыта, неизвестно, какое именно. Случайная величина Х называется дискретной (прерывной), если множество ее значений конечное или бесконечное, но счетное.
Другими словами, возможные значения дискретной случайной величину можно пронумеровать.Описать случайную величину можно с помощью ее закона распределения.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения может иметь разные формы. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.
Простейшей формой задания закона распределения дискретной случайной величины X является таблица (матрица), в которой в порядке возрастания перечислены все возможные значения случайной величины и соответствующие их вероятности, т.е.

или
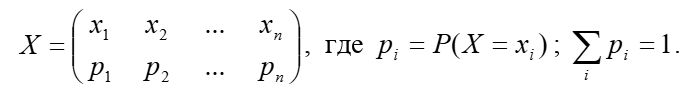
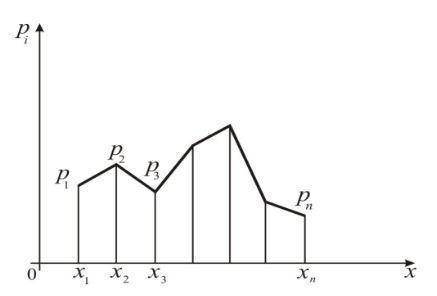
Такая таблица называется рядом распределения дискретной случайной величины X. Графическое изображение ряда распределения называется многоугольником (или полигоном) распределения.
Одним из наиболее удобных и универсальных способов задания закона распределения случайной величины X является функция распределения.
Функцией распределения (или интегральной функцией распределения) случайной величины X называется функция , которая для любого числа равна вероятности события, состоящего в том, что случайная величина примет значение, меньшее, чем , т. е. .
Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее данной точки x.

Функция распределения обладает следующими свойствами:
1. 0 ≤ F(x) ≤ 1;
2. F(x) - неубывающая функция, т. е. F(x₂) ≥ F(x₁), если x₂ > x₁;
3. F(-∞) = 0, F(+∞) = 1;
4. F(x) - непрерывна слева в любой точке x, т.е. F(x-0) = F(x), x∈R;
5. P(a ≤ X < b) = F(b) - F(a);
Функция распределения дискретной случайной величины имеет вид:
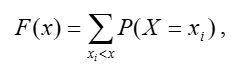
где суммирование ведется по всем индексам. Для дискретной случайной величины функция распределения есть разрывная ступенчатая функция, непрерывная слева.
Математическим ожиданием (или средним значением) (или ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
Если дискретная случайная величина X принимает конечное число значений x₁, x₂, ..., xₙ, то ее математическое ожидание находится по формуле
M(X) = Σi=1n xi · pi
Свойства математического ожидания:
Математическое ожидание алгебраической суммы случайных величин равно алгебраической суме их математических ожиданий.
Постоянныймножитель можно выносить за знак математического ожидания. Так век постоянная С не зависит от того какое значение примет сл. величина X, то имеем
М(СХ)=М(С)×М(Х)=С×М(Х)
Дисперсией (рассеянием) (или ) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X) = M(X - mₓ)²
Свойства дисперсии:
Постоянную можно выносить за знак дисперсии с возведением в квадрат.
D(aX) = a²D(X)
Если случайные величины Х и У независимы, то
D(X+Y) = D(X) + D(Y)
Средним квадратическим отклонением случайной величины называется величина
σ(X) = √D(X)
Среднее квадратическое отклонение есть мера рассеяния значений случайной величины около ее математического ожидания.
ˏˋ°•*⁀➷ Тема 11: Непрерывные случайные величи
Непрерывной случайной величиной называется случайная величина, бесконечное несчетное множество возможных значений которой есть некоторый промежуток (конечный или бесконечный) числовой оси.
Интегральной функцией распределения непрерывной случайной величины X называется функция F(x), которая для любого числа x∈R равна вероятности события, состоящего в том, что случайная величина примет значение, меньшее, чем x, т. е. F(x) = P(X < x).
Плотностью распределения непрерывной случайной величины X (или плотностью вероятности, или просто плотностью) называется функция φ(x) = F'(x)
Функцию φ(x) называют также дифференциальной функцией распределения.
Плотность распределения любой непрерывной случайной величины неотрицательна, т. е. φ(x) ≥ 0; обладает свойством нормированности:
∫-∞+∞ φ(x) dx = 1; x→±∞ φ(x) = 0
График функции φ(x) называется кривой распределения.
Функция распределения F(x) выражается через плотность распределения формулой
F(x) = ∫-∞x φ(t) dt
Вероятность попадания непрерывной случайной величины в промежуток определяется равенством:
P(a ≤ X < b) = ∫ab φ(x) dx
Математическое ожидание непрерывной случайной величины X с плотностью вероятности φ(x), находится по формуле
M(X) = ∫-∞+∞ x φ(x) dx
Если X - непрерывная случайная величина с плотностью φ(x), то
D(X) = ∫-∞+∞ (x - mX)² φ(x) dx (или D(X) = ∫-∞+∞ x² φ(x) dx - mX²)
Средним квадратическим отклонением случайной величины называется величина
σ(X) = √D(X)
Равномерный закон распределения
Непрерывная случайная величина X имеет равномерный закон распределения на отрезке [a, b], если ее плотность вероятности φ(x) постоянна на этом отрезке и равна нулю вне его:
φ(x) = { 1/(b-a) при a ≤ x ≤ b; 0 при x < a, x > b }
Равномерное распределение случайной величины X на участке [a, b] (или (a, b)) обозначают следующим образом: X ∼ R[a, b].
Функция распределения F(x) для равномерно распределенной случайной величины X, имеет вид:
F(x) = { 0 при x ≤ a; (x-a)/(b-a) при a < x ≤ b; 1 при x > b }
Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины X, имеющей равномерное распределение, находятся по формулам:
M(X) = (a + b)/2
D(X) = (b - a)²/12
σ(X) = (b - a)/√12
ˏˋ°•*⁀➷ Тема 12: Числовые характеристики вариационного ряда
Вариационным рядом называется ранжированный в порядке возрастания ряд значений (вариантов) с соответствующими им частотами.
| Значения xi | x1 | x2 | ... | xk |
|---|---|---|---|---|
| Частота ni | n1 | n2 | ... | nk |
| Частости wi = ni/n | w1 | w2 | ... | wk |
Выборочная средняя:
X̅ = (∑i=1m xi · ni) / n
Выборочная дисперсия находится по формуле:
DB = (∑i=1m xi² · ni) / n - X̄²
Выборочное среднее квадратичное отклонение:
σB = √DB
Размахом вариации называется число:
R = xmax - xmin
Модой вариационного ряда Mo называется то из значений 1x, 2x, 3x, …, nx, которому соответствует наибольшая частота.
Медиана Me — это значение варианты, которая является серединой вариационного ряда. Если количество вариант четное, то медиана вычисляется как среднее двух вариант, находящихся в середине множества.